Unsere Welt besteht aus vielen verschiedenen Formen und Strukturen. In der Topologie, einem Zweig der Mathematik, beschäftigt man sich damit, wie diese Formen sich verhalten, wenn sie kontinuierlich verformt werden. Topologie untersucht also die Eigenschaften von Objekten, die bei solchen Verformungen – wie Dehnen oder Biegen – unverändert bleiben, solange dabei nicht geschnitten oder geklebt wird.
Was bedeutet das genau?
Topologie:
In der Mathematik bezieht sich das Wort „Topologie” auf die Lehre von den Eigenschaften und Strukturen, die bei kontinuierlichen Verformungen erhalten bleiben.
Kontinuierliche Verformung:
Dies bedeutet, dass ein Objekt beliebig gedehnt oder gebogen werden kann, ohne dass es dabei zerrissen oder zusammengeklebt wird. Topologische Eigenschaften ändern sich nicht durch solche Verformungen.
Eigenschaften:
Topologische Eigenschaften sind beispielsweise die Anzahl der Löcher oder die Verbundenheit eines Objekts. Ein bekanntes Beispiel ist, dass ein Donut (Torus) und eine Kaffeetasse mit einem Henkel topologisch äquivalent (homöomorph) sind, weil beide ein Loch haben. Das heißt, durch Dehnen, Stauchen, Verbiegen oder Verzerren kann man einen Gegenstand zu einem anderen umformen.
Robustheit gegen lokale Störungen:
In der Physik nutzt man die Prinzipien der Topologie, um Materiezustände zu beschreiben, die durch ihre globalen Eigenschaften charakterisiert werden und nicht durch lokale Störungen verändert werden können. Solche Zustände sind robust gegenüber kleinen Defekten oder Unreinheiten.
Ein faszinierendes Beispiel ist der Quanten-Hall-Effekt. Hier zeigt sich, dass der elektrische Widerstand in zweidimensionalen Elektronensystemen bei sehr niedrigen Temperaturen und starken Magnetfeldern in diskreten Schritten quantisiert ist. Diese Quantisierung ist eine direkte Folge der topologischen Eigenschaften des Systems.
Die Forschung in der Topologie hat weitreichende Anwendungen in der modernen Physik und Technologie. Sie hilft uns, neue Materiezustände zu entdecken und zu verstehen, wie diese für innovative Technologien genutzt werden können. So trägt die Topologie entscheidend dazu bei, unsere Kenntnisse über die grundlegenden Eigenschaften der Materie zu erweitern.
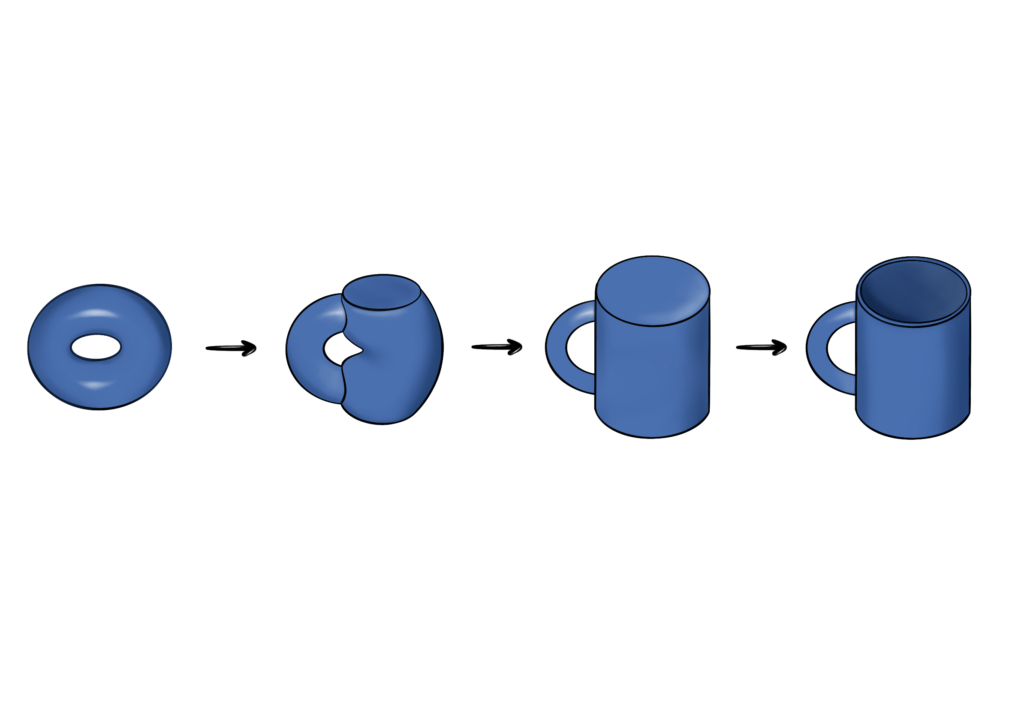
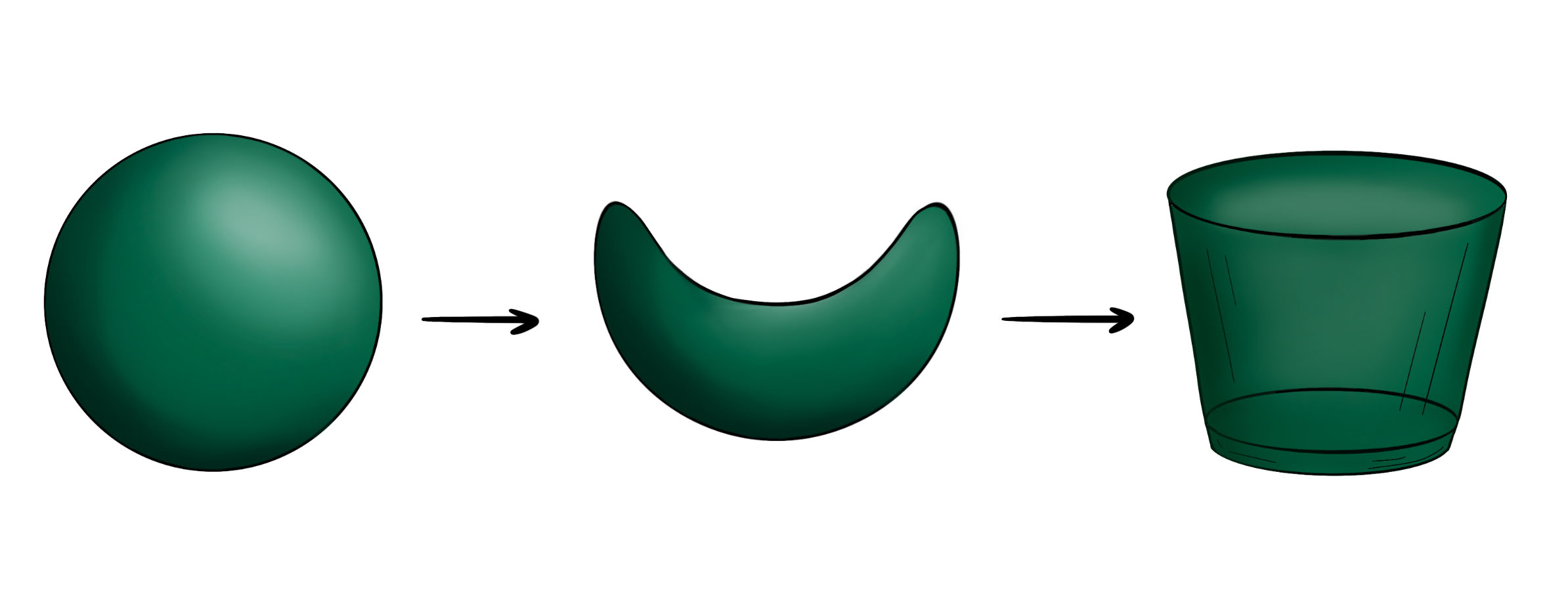
Drei Beispiele für Objekte mit gleichen topologischen Eigenschaften – durch Verformung, Dehnung, Stauchung, etc. kann z.B. aus einer Kugel ein Becher oder aus einem Donut eine Tasse mit Henkel werden.
